Figuring Numbers

 

Introduction

Gematria is founded upon numerical relationships between words and phrases already related by meaning. The numerical relationships may be a simple equality, the sharing of important factors or another mathematical property, such as the numerical properties of geometric figures. [1]

Regular arrangements of objects such as coins on a surface can give rise to pixelated representations of plane figures such as the triangle, square, pentagon and hexagon. Similarly, spheres or cubes can be regularly packed to build solid objects such as the cube, tetrahedron and pyramid. Ever larger versions of these figures can be created, therefore each geometric figure is associated with a sequence of numbers. All such numbers are described as figurate.
 

Triangular Numbers

The first ten members of the sequence of triangular numbers are illustrated below as pixelated triangles. Note that all sequences of figurate numbers begin with a single unit, then grow in one direction from it, unlike central triangles, described below, which grow outwards from a central unit. The second member of each sequence is always the first to show its characteristic shape. 

 

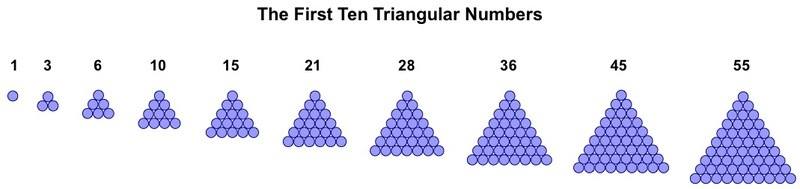
The triangular numbers are created by simply adding the natural numbers in order, something that can be intuited by observing that the positional value of any triangle in the sequence is the same as the number of units along its base.

Each triangle in the sequence is given a positional value. For example, triangle 10 is the fourth in the sequence and can alternatively be referred to as T(4). The formula for calculating the nth triangular number is as follows: T(n) = 1/2n(n + 1).

Several plane figures related to triangles, each with their own numerical sequence, are illustrated below.

 

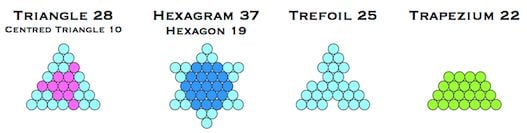
 Triangle 28 is a member of a special class of triangular numbers dubbed the G-triangles [3]. Every figure above is in fact directly or indirectly derived from the G-triangles. 

 

Plane Figures: Square, Pentagonal, etc

Units can pack in square formation to give more plane figures: principally the square and the diamond. This idea can be extended to pentagonal formation, hexagonal formation, etc, to give further sequences of figures. 

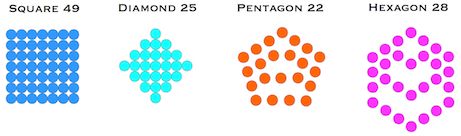
There are many hidden relationships between these fundamental shapes. For example, 

a) the pentagonal numbers are numerically equal to the trapezium numbers, and

b) every second triangular number is also a hexagonal number. 

 

Centred Figures

Sequences of figures that grow outward from a central unit can also be created.

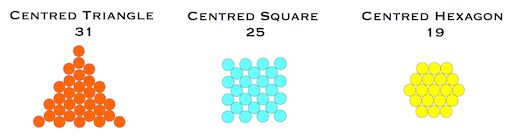
Again, there are hidden connections between these figures. We already saw how centred triangles and centred hexagons can be created from non-centred triangles. Centred squares are simply diamonds rotated by 45 degrees. 

 

Solid Figures

Regular solids, such as the cube, tetrahedron and square pyramid can similarly be represented by tightly packed arrangements of spheres or cubes. As with plane figures, all solids are associated with their own numerical sequence.

 

 

 

Polyfiguracy

Some numbers can be represented by two or more regular shapes. These are known as polyfigurate numbers. If two shapes can be created the number is bifigurate, three shapes trifigurate, etc.

 

 

 

Structural Properties

All plane and solid shapes of any complexity have structural properties. Some basic structural properties of the triangle and the cube are shown here.

 

 

 

Sequences of Figurate Numbers

The first 16 terms of some regular plane figures and solids are shown in the table.

 

 

 

 

Bill Downie 17/5/04

Latest update 6/9/20

Notes 

1.By 'geometric figures' I mean regular plane and solid figures (polygons and polyhedrons), including fractal snowflakes and other star figures, that can be created by tightly packed arrangements of regular units. I now include figures packed in triangular, square, pentagonal and hexagonal formation and all centred figures.

2. Trapezia of different heights can be constructed, but the one shown has equal numbers of units on the top and side and could therefore be said to be regular. It is numerically equal to the pentagonal numbers.

3. This term was coined by Vernon Jenkins.