The 'G' Triangles

The simplest sequence of figurate numbers is the triangular numbers: 1, 3, 6, 10, 15, 21,18 . . . . They are called 'triangular' because they can be depicted as counters arranged into triangles, as shown here.

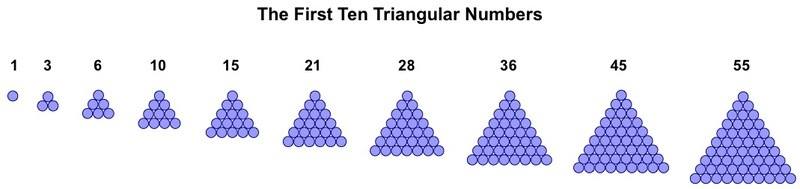
The triangular numbers are produced by the elementary procedure of summing the natural numbers: 1, 2, 3, 4, 5 . . ., which are the rows of counters that can easily be seen by running your eye down one of the larger triangles from the apex.

An example in everyday life is the balls on a pool table, after they have been placed in the triangular rack at the beginning of a game,

 

G-Triangles

Among the triangular numbers are a special class, termed 'G-triangles' by Vernon Jenkins. I will use this terminology here. 'G' means 'generator' and this is because each of these triangles can self-intersect to generate a hexagram/hexagon pair, or Star of David, as illustrated below with triangle 55, one of the G-triangles.

 

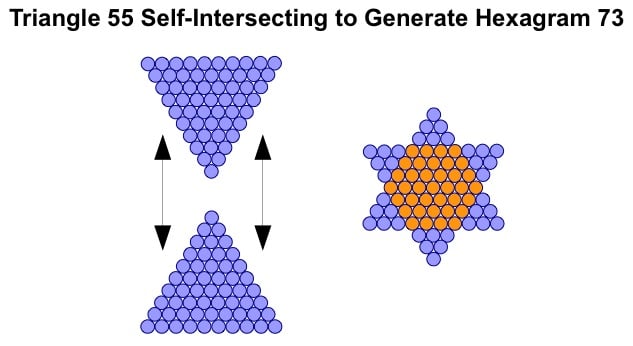
The internal hexagon is revealed by using a second colour for superimposed counters.

Every third member of the triangular number sequence is a G-triangle. These have one central counter, around which the triangle can flip to create a perfect inverted copy for merging. The other triangles have either three or six counters at their centre and therefore cannot be merged with an inverted copy without the counters overlapping.

The first ten numerical triangles are shown below, along with the Star of Davids created by the subclass of G-triangles. 

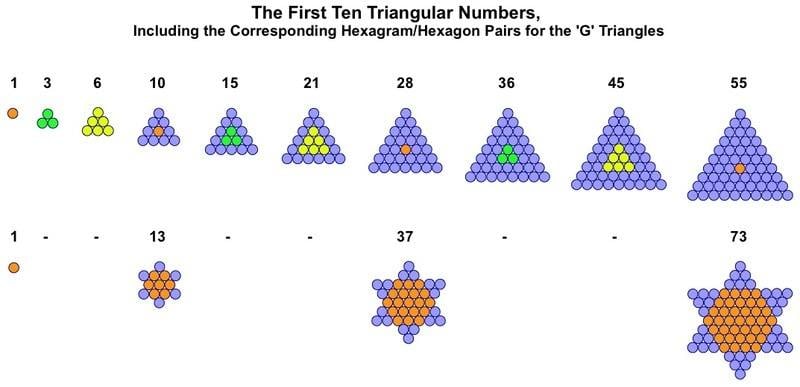
Hexagram/hexagon pairs can themselves be the basis for fractal snowflakes.

 

G-Triangles and Trefoils

The G-Triangles are also the basis for a series of trefoils (a word which means 'three-leaved plant'). Like their G-triangle parents these figures have a single counter at their heart, from which spring three diamond-shaped leaves.

 

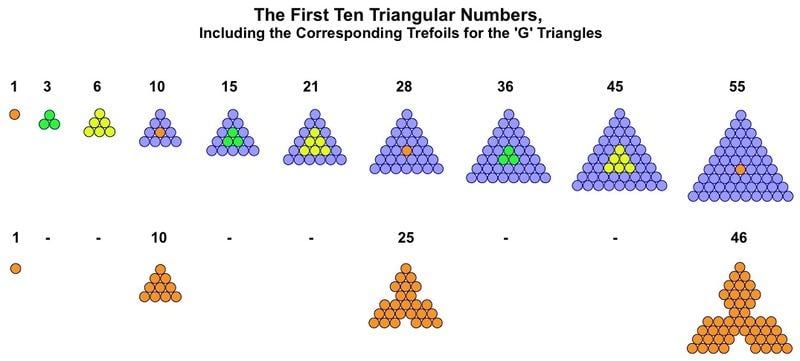
Each leaf of the trefoil is a square/diamond. Like its associated G-triangle this type of trefoil can self-intersect to form a hexagram, although with a different the internal structure this time.

 

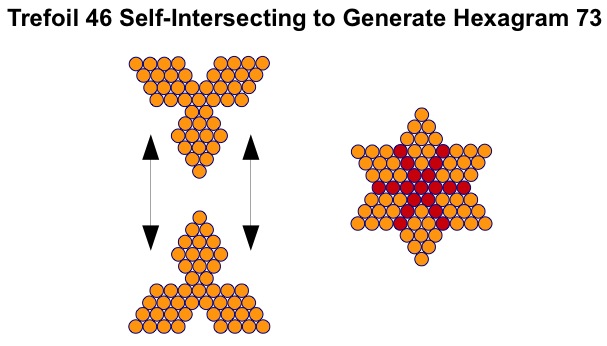
The star figure within the hexagram is created like the hexagon in the Star of David by showing superimposed counters.

The trefoil is the first step in the iterative process that creates the Koch antisnowflake, starting with a triangle, and is therefore analogous to the Star of David, which is the first step in the creation of the Koch snowflake.

 

G-Triangles and Centred Triangles

From the G-triangles the entire sequence of centred triangles can be created, by subtraction of appropriate units. Here again are the first few triangular numbers, showing the G-triangles and their corresponding centred triangles.

 

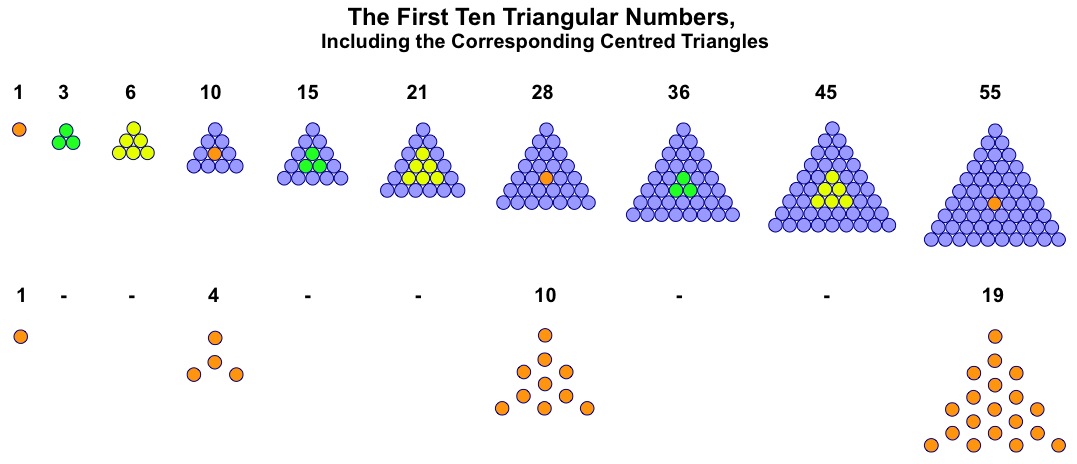
 So the G-triangles generate further interesting figures, many of which have been utilised in the New Bible Code.

 

G1, G2 and G3 Triangles

Recent discoveries have led to to see that every member of the sequence of numerical triangles can be transformed into related figures through simple iterative functions. 

As shown above, all G-triangles (10, 28, 55 . . . .) can self-reflect to form a hexagram, which non-G-triangles cannot, since they lack a single unit at their centre. However, all triangles can form a trefoil, once the rules are understood. [1]

G-triangles form the most natural type of trefoil, where all three leaves are joined by a single, central unit. The other two types, with triangles 3 and 6 at their centres, form two corresponding families of trefoil. The details are given below, for the first few triangles.

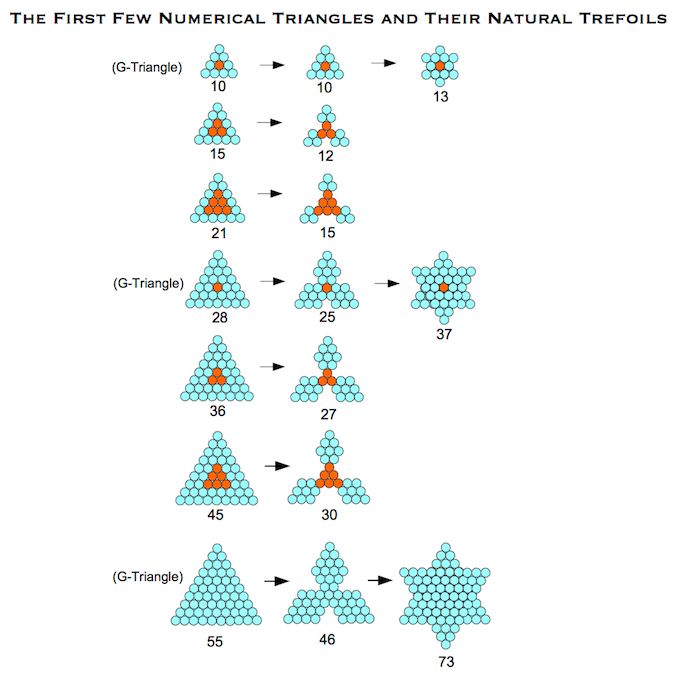
 These numerical triangles and trefoils are the pixellated approximations of the first iterations of Koch snowflakes and antisnowflakes. Just as non-G-triangles can naturally produce trefoils, some of these trefoils can be taken further steps towards the Koch antisnowflake.

 

Bill Downie 15/7/15

Latest update 29/10/21

 

 Notes

1. Numerical triangles form digital images of figures. Unlike triangles from plane geometry, these figures can only be manipulated in certain ways, depending on the number of units in the figures