A Lily Lattice
Introduction
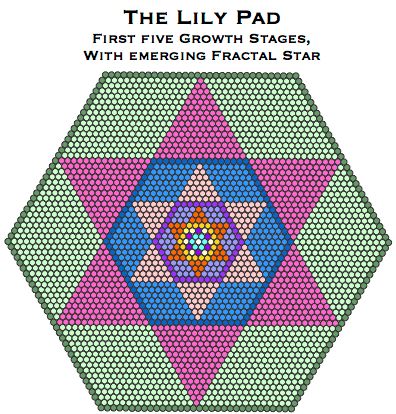
The Lily Pad, shown above, is a record of five stages of the geometric growth of hexagram/hexagon pairs, starting with a single unit. There is more than one way of growing the pad and the 'flowers' within; these superimposed upon each other act as a template from which a wide range of geometric figres symbolising the Trinity can be cut.
Two types of 'flower' are involved:
- hexagram/hexagon pairs - more usually created by the self-intersection of G-triangles;
- star hexagram/star hexagon pairs - more usually created by the self-intersection of centred triangles.
The image above shows the first type. This version of the Lily Pad turns out to have some fascinating mathematical properties, which take us further into the garden of discovery.
A Recursive Excursion
The Lily Pad has some interesting mathematical properties.
1. The figure is a pixelated image of a star fractal, shown in outline form here.
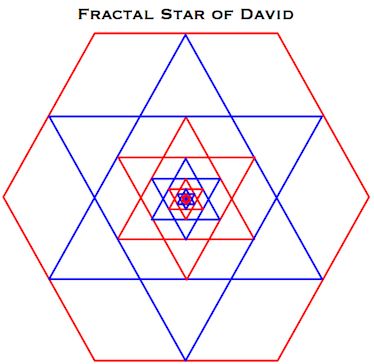
This fractal is created in plane geometry by the following recursive function:
- i) Draw a Star of David.
- ii) Inside the internal hexagon draw another Star of David, the points of which touch the outline of the hexagon.
- iii) Repeat this process ad infinitum.
In numerical geometry, the more terms we add to the sequence, the closer we come to the true fractal.
Fractal geometry is the geometry of nature. Within the code, fractals such as the Koch Snowflake are employed as a metaphor for life and growth - so we are off to a good beginning.
2. The phenomenon of geometric growth emerges naturally from the growth of the lily. In fact that was one of the reasons I chose the water lily metaphor, because many plants, including water lilies, exhibit geometric growth during their vegetative stage, doubling in size over a set period. In the lily pad the sides of the hexagons double with every growth stage. So we have
| Stage | Hexagon | Side |
| 0 | (1) | (1) |
| 1 | 7 | 2 |
| 2 | 37 | 4 |
| 3 | 169 | 8 |
| 4 | 721 | 16 |
| 5 | 2977 | 32 |
In the hexagrams the doubling at each stage is shown in the number of units from point to point inclusive.
The sequence of hexagons formed at each stage (7, 37, 169, 721, 2977, . . . .) is Sloane's sequence A169726, minus the first entry. [1]
3. The hexagrams at each growth stage consist of an internal hexagon surrounded by six triangles. As the sequence progresses, the index of these triangular spurs gives the sequence of Mersene numbers, given by the formula 2^n -1, where n is an integer. The triangles are shown below with the equivalent Mersene number.
| Growth Stage | Triangular Spur | Index | Mersene No. (2^n - 1) |
| 1 | 0 (T0) | 0 | 0 (2^0 - 1) |
| 2 | 1 (T1) | 1 | 1 (2^1 - 1) |
| 3 | 6 (T3) | 3 | 3 (2^2 - 1) |
| 4 | 28 (T7) | 7 | 7 (2^3 - 1) |
| 5 | 120 (T15) | 15 | 15 (2^4 - 1) |
The introduction of Mersene numbers is a clue to the most fruitful mathematical connection of all.
4. The pattern of triangles radiating out from the hexagrams hides a startling connection. If we take a triangular slice of the lily pad, shown below, and place it beside Pascal's triangle and a pixelated image of the Sierpinski triangle, we see that all three figures share the same 'spine' of inverted triangles.
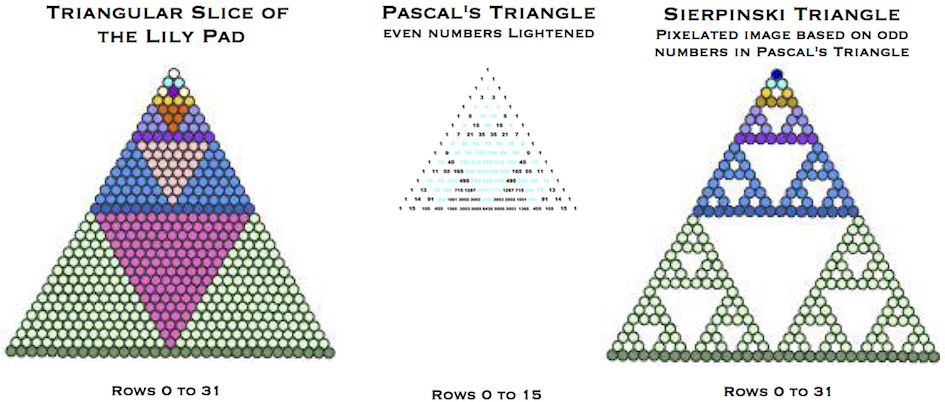
The central spine of inverted triangles is common to all three figures, but counterintuitively the triangles are all produced by different methods.
- Within the Lily Pad they are formed by geometric growth.
- Within Pascal's triangle they are formed by the even numbers within it, lightened in the above illustration. [2]
- Within the pixelated Sierpinski triangle they are formed as holes by the removal of the triangular cores at each stage of an iterative process.
One of the remarkable properties of Pascal's triangle itself is that it can be transformed into the Sierpinski triangle by the simple removal of the even numbers. The more of Pascal's triangle taken, the more closely the resulting figure approaches the fractal.
Like the Lily Pad, Pascal's triangle contains the Mersene numbers, found this time by progressively summing the numbers down to each row from the apex. In fact all three figures harbour the Mersene numbers as the indexes of the triangles forming the central spine.
The Sierpinski triangle image also contains the powers of three, on which it is built. [3]
A Sierpinski Lattice
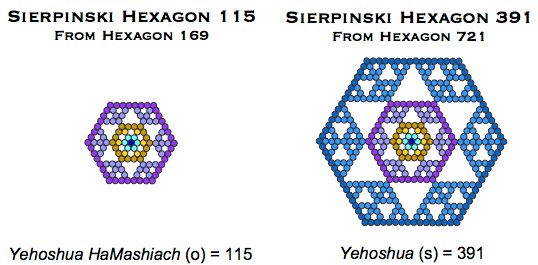
The full Lily Pad is a hexagon, so to see if there was any deeper connection between them I decided to create a hexagon from six versions of my pixelated Sierpinski triangle. The resulting lattice has 1267 units. [4]
If hexagon 2977 is a lily pad then this gossamer wonder is a lily pad after the ravages of a caterpillar. It also resembles a leaf skeleton or a lattice pie.

This site has more on the Sierpinski triangle and the hexagon made from six such triangles.
Slices of Lattice Pie
Consistent with the code's use of fractal snowflakes as a metaphor for life and growth in a garden, and with the status of its parent Lily Pad as a template of divine gematria, this hexagonal lattice has the following numbers built into its structure.
Two more structural components of the hexagonal filigree are worth noting.

If we compare the growth of the Sierpinski variant of the Lily Pad with the growth of the Lily Pad itself, we see two diverging numerical sequences (both found on Sloane's Online Encyclopedia of Integer Sequences).
| Growth Stage | Lily Pad | Sierpinski Hexagon |
| 1 | 7 | 7 |
| 2 | 37 | 31 |
| 3 | 169 | 115 |
| 4 | 721 | 391 |
| 5 | 2977 | 1267 |
| OEIS Sequence | A169726 | A091344 |
In lining up the two sequences we see that hexagonal lattices 115 and 391 are derived from hexagons 169 and 721, strengthening an already dense network of connections between these hexagons, both born from G-triangles, and the gematria of Jesus Christ.
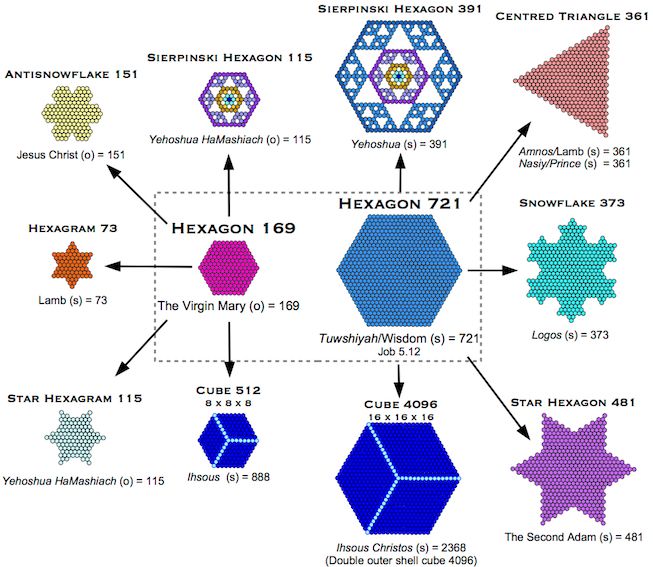
Further connections are found on several pages of this site, including here and here.
The more I study the Lily Pad the more of mathematical interest I see and the more important to the New Bible Code it becomes. The hexagonal lattice in particular, through the gematria it embodies and its Star of David pattern, symbolises the Christ and is another geometric witness to the glory of God. [5]
In the next page I'd like to tie it all together by showing a transformation of Pascal's triangle that had been waiting to be unlocked since I was given the Key to the Code in 2001.
Bill Downie
22/7/20
Notes
1. This was found by Alice Kleeva in 2010 as another mathematical construction. This article by Robert Munafo summarises her work. Thanks to John Elias for pointing out this connection.
2. I've show only the first 16 rows here (0 to 15), as the numbers are too large to easily fit into later rows.
3. The powers of three are found within the Sierpinski Triangle image by counting the number of units down to each triangle base (coloured darker than the rest). This gives the sequence 1, 3, 9, 27, 81, 243 . . . , which is 3^0, 3^1, 3^2, 3^3, 3^4, 3^5, . . . .
4. Sierpinski discussed this type of hexagon in 1915.
5. 1267, the number of counters in the hexagon, is a close anagram of 1276, standard value of 'Holy Spirit'.
