A Flurry Of Snowflakes

 

Introduction

A fresh snowfall is one of nature's miracles, brightening the drabbest landscape, adding excitement to the dullest day and forcing us to acknowledge its transforming power and timeless beauty. A snowfall is of course an accumulation of innumerable snowflakes, which are themselves aggregates of tiny snow crystals. Under a microscope snow crystals turn out to be fascinating objects. Peering through the lens, the viewer enters a diamantine realm of pristine beauty and infinite variety. Before long, it will be observed that snow crystals show an interesting six-fold symmetry. No matter how dissimilar two crystals might be, they will both depend on the number six for their basic structure [1]:

     

Underlying the natural complexity on display in this beautiful photograph is the geometric form of the hexagon. The hexagonal symmetry of the snowflake is also seen in a purely     mathematical object, known as the Koch Snowflake.

 

The Koch Snowflake

The intricate structure of natural snow crystals is described in mathematical terms by the language of fractal geometry, because snow crystals approximate to a class of geometric figures known as fractals. These objects have mind-blowing properties such as fractional dimension (hence ‘fractal’) and self-similarity (they display similarities of form at different scales). The prototypical fractal snowflake is the Koch snowflake, created by the following iterative process [2]:

Starting figure:

an equilateral outline triangle.

Iteration 1:

a) Subdivide each side of an equilateral triangle into three equal portions.

b) Draw an equilateral triangle which has the central portion as its base and points outwards from the triangle;

c) subtract the base.

Iterations 2, 3, 4 etc:

Repeat iteration 1 with each side of the new figure.

The first two steps of this process are illustrated below, along with the Koch snowflake itself [3]: 

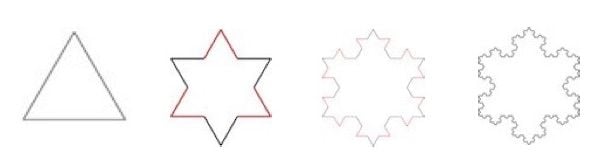
Note that the first step creates an outline hexagram. This is a clue to a more intuitive way of creating the Koch Snowflake, by merging the triangle, and each triangle thereafter created, with an inverted copy of itself, as shown here:

This method also has the feature of creating internal structure within the fractal. So now after step 1 we see the Star of David proper, with an internal hexagon clearly delineated. Steps 2 and 3 create closer approximations of the Koch snowflake, nested within which are snowflakes of a different design, known as Koch antisnowflakes. Standalone versions of these antisnowflakes can be created from a hexagon by a variation of the process leading to the Koch snowflake, where we draw triangles that points inwards, rather than outwards.

 

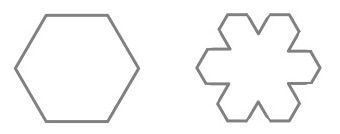
Antishowflakes can also be created from triangles. The first step creates a trefoil, meaning three-leaved plant, as can be seen below:

 

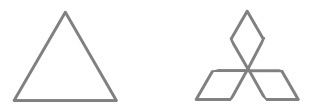
 Trefoils are found encoded in the first five verses of the NIV Bible.

 

The Koch Snowflake Emulated

The creation of the Koch Snowflake can be emulated for one or more steps with every third triangle in the triangular number sequence, dubbed G-triangles (meaning 'generator triangles'), which are those with a single unit at their geometric centre [4]. This is accomplished by the merging of a G-triangle, and any G-triangle thereby created, with an inverted copy of itself, as just shown with outline triangles. For instance, triangle 28 self-intersects to give a hexagram/hexagon pair (Star of David) with 37 and 19 units:

 

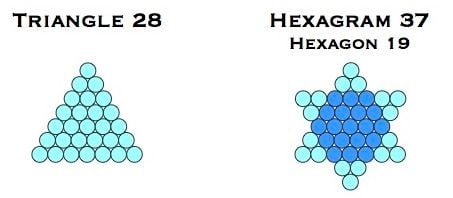
Star of David 37/19 is the seed for the Creation snowflake.

Triangle 28 can only be taken this one step towards the Koch snowflake. The first triangle that can be taken two steps towards the Koch Snowflake is triangle 91 (T13). This process is illustrated below:

 

 

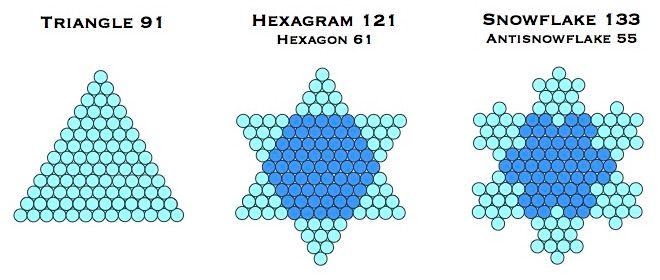
The Internal Snowflake

The internal antisnowflake, with 55 units, can also be created ‘standalone’ by the variation of iterative process shown above, where we draw triangles pointing into the figure. This is illustrated below:

 

 

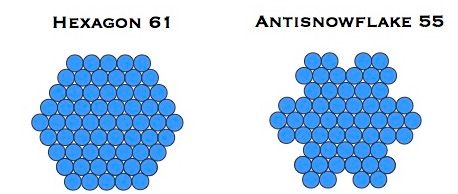
Building the Snowflake from Crystals

Real snowflakes are accretions of smaller crystals. Similarly, these emulations of the Koch snowflakes and antisnowflakes can also be built from two simple geometric snow crystals, as seen here with antisnowflake 55:

 

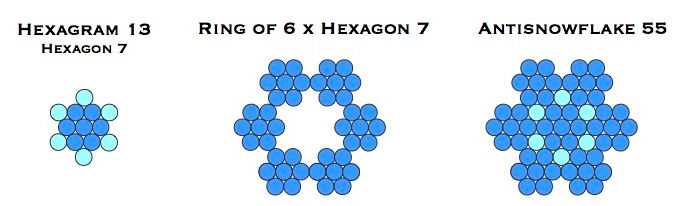
Here we see six hexagons surrounding a central hexagram, the seed for this snowflake. This 6-plus-1 pattern is familiar to us in the Creation story, in which God manifested the heavens and the earth in six days before resting on the seventh day. The next step is to surround antisnowflake 55 with 6 x hexagram 13 to create snowflake 133.

 

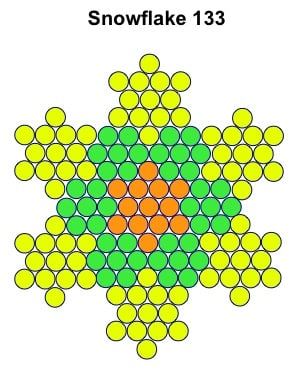
The process of accretion can be continued indefinitely with the above figure, to create a sequence of snowflakes that grow ever closer in structure to the Koch snowflake itself. In fact there are an infinite number of Koch snowflake sequences, each growing from a seed that is a member of the hexagram sequence (1, 13, 37, 73, 121, . . . .). The next sequence begins with hexagram 37, giving rise to the following antisnowflake after one iteration.

This figure is a kind of 'strange attractor' for gematria related to Jesus Christ:

Jesus Christ (o) ......= 151

Holy Spirit (o) .........= 151

The Incarnation (o) = 151

Jesus is Lord (o) ....= 151

Christ the King (o) .= 151

In this manner a variety of fractal snowflakes and antisnowflakes can be created, which turn out to be a unique and vital feature of the New Bible Code. 

 

Snowflakes from Centred Triangles

Like their non-centred equivalents, centred triangles can also be taken through the iterative Koch snowflake process, to again produce pixellated snowflakes and antisnowflakes. The rules are slightly different for centred triangles, though, the biggest difference being that every centred triangle gives rise to a snowflake and antisnowflake, a consequence of the fact that every centred triangle can be matched to a G-triangle (those with a central unit, coloured red here).

 

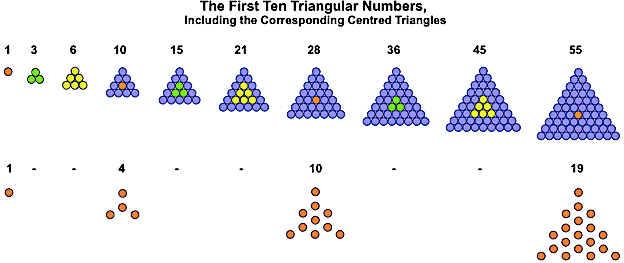
Here are the first iterations in the creation of these new snowflakes and antisnowflakes: the Star of David and the trefoil. To distinguish them from their non-centred triangle equivalents, I've named them Bethlehem stars and trefoils, as shown below. [5]

  

 

 

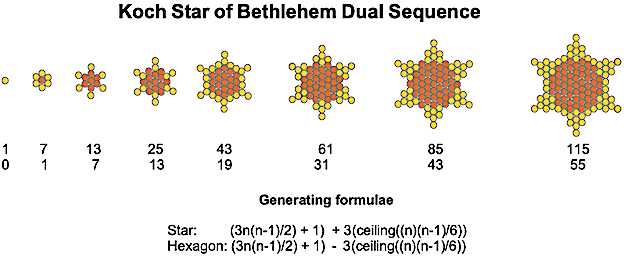
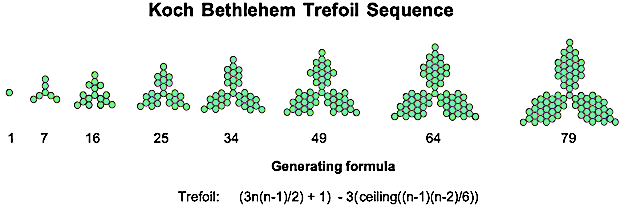
I've included the generating formulae too, since they aren't found on the OEIS. [6]

 

Bill Downie 17/5/04

Latest update 24/5/23

 

Notes

1. Image courtesy of SnowCrystals.com.

2.. In mathematics an iterative process is one in which, at each step of the process, the same operation is repeated on the outcome of the previous step.

3. For the mathematically-inclined reader, the dimension of the outline of the Koch snowflake is log4/log3, or 1.261859... Amazing but true.

4. This nomenclature is due to Vernon Jenkins. 

5. The stigma of the six-petalled flower of Bethlehem are rotated 30 degrees to the petals, the same angle at which the centred triangles lie within the non-centred triangles.

6. I worked them out myself but, since I'm not a professional mathematician, I offer them tentatively. They certainly give the correct results. The ceiling function simply raises any non-whole number up to the next whole number. So 2.4 becomes 3.